JOE STUDENT

Instructions for:

Lab Exercise #1: Spatial Analysis of a survey on attitudes about Population Growth In Santa Barbara County

Background

In this dataset you should find an ESRI readable coverage of Santa Barbara county 1990 census data at the Tract and block-group level. This dataset is the demographic backdrop for performing a spatial analysis of geo-referenced survey data. I conducted a survey of registered voters in Santa Barbara County in 1995 (this work was my M.A. thesis). You should also find a word document that contains the survey instrument I used. It consisted of almost one hundred questions that characterized various demographic attributes of the respondent (age, education, income, sex, religiosity, etc) in addition to their attitudes to a multitude of questions about population, immigration, and the social, economic, and environmental impacts of population growth. 3,000 records were randomly selected from the registered voters of Santa Barbara County. All of these people were called on the phone and agreed to respond to this survey by mail. 750 responses were returned. You should find a file which contains the coded responses of these 750 odd people. The survey instrument requested respondents to provide the closest street intersection to their home location. You will use this information to geo-code the survey. By geo-coding (aka ‘address matching) this survey you can enable a ‘spatial’ analysis of this survey. The non-geo-coded responses lend themselves to many traditional statistical analyses; the geo-coded survey allows for many more traditional statistical analyses that incorporate spatially specific attributes. Your mission is to answer the following spatial and a-spatial questions using the information contained in this dataset.

Assessing ‘Representativeness’ of the survey respondents (1-6)

Preliminary instructions:

Copy all data on CD to a location on hard disk or server
Change permissions on ALL files from Read only in Windows Explorer (right click on file, open permissions dialog box, uncheck read only)

1) Were the home locations of the respondents to this survey spatially random?

(you don’t have to do the analysis on this question, just answer it, & explain how you would have done the analysis if you had to)

· Open ArcView and start a new project with a new View.

· Add all of the shapefiles found on CD \spatialstatsclass\sbcopopsurvey\spatialdata

· Look at distribution of respondents

· It may be obvious that the distribution is not random, but how could you quantify this? (Hint: The X² test compares an observed value to an expected value to assess randomness, how could you create these values?)

· Save project

2) Were the home locations of the respondents to this survey random with respect to population density? (you do have to do the analysis for this one)

A. ArcView data summary

· Open ArcView

· Open Saved project from question 1.

· Click on Tables in the project window of ArcView

· Open Tract table (sbcotractsdemog)

· Open survey table (surveyresultsneq724)

· Click on “shape” heading in Tract Table

· Click on “shape” heading in Survey table

· Press Join button in tool bar. The tract table data will be appended to the Survey table data

· Click on “Tract90” heading in Survey table

· Press Sort

· Press “field” then “summarize”, click on OK (use default parameters)

· Open Summary table, highlight “Tract90” in heading

· Open Tract table, highlight “tract90” heading

· Press Join button in tool bar

· Export Tract table with all joins as a .DBF extension (File---Export)

B. Cleanup in JMP

· Open JMP to clean up file for processing

· Open file exported from ArcView

· Delete duplicate rows of 74’s and 54’s

· Select all question columns, Edit—Search—Find—6---replace all with a period (.)

· Save cleaned file in DBF form

C. Analysis in Excel

· Open Excel

· Use “Person” column for population counts, this is the “Observed” number

· Create a new column, with appropriate column heading “Expected”

· Sum the Persons column to calculate total population

· Type formula in new Expected column to calculate expected number of respondents in each tract: Persons (column)/ total population (summarized field: type in the number)*483 (number of tracts)

Perform X² test: x² = Σ(O-E)²

· Create a column to perform Chi square test. In it create the following formula (observed-expected)²/expected, summarize this column for the X²statistic.

· Using the Chi square table, and the result from the formula determine if the result falls within the 95% confidence level to determine randomness

3) What level of spatial aggregation (tracts or block-groups) is more appropriate to answering question #2. Explain.

Hint: Think about the size of tracts and blocks, and assumptions of the Chi-square test.

4) How would you test the following?: a) Is the age distribution of the respondents to this survey significantly different than the age distribution of the population of Santa Barbara County? b) Is the income of the respondents to this survey significantly different than the population of Santa Barbara County? c) Are the political party, ethnicity, and gender distribution of the respondents to this survey significantly different from the population of Santa Barbara County? (don’t actually do the tests just explain your best effort if you had to)

Hint: What tests should you use and why?

5) What kinds of problems do you run into when trying to answer the questions posed in #4?

Look at answers and evaluate. Hint: What data types are you dealing with?

6) Are the respondents to this survey age and income independent? Would you expect them to be? Is this a parametric or non-parametric test?

Hint: What kind of data are you dealing with?

· JMP, open data surveyresultsneq724

· Change income column to nominal (Double click on column heading---double click on data type)

· Change age to continuous

· Fit y by x (Analysis pull down)

· x factor to income, y factor to age

· Select Compare Means –Tukey Test all pairs

· Evaluate means, probability

· What factors could account for the difference in means?

Simple Demographic Comparisons (7-11)

7) Based on the responses to the question: ‘Abortion should remain legal as defined in “Roe v. Wade”?’; are Democrats significantly more ‘Pro-Choice’ than Republicans?

· Open surveyresults724 in JMP

· Select polparty, change to nominal

· Select p3_9, change to continuous (if necessary)

· Analyze--Fit Y by X

· Y P3_9, X polparty

· Click on UL Red triangle, select Means/Anova/T test

· Evaluate test results

8) Along a similar vein, are Women more ‘Pro-Choice’ than Men? (according to this survey)

· Fit Y by X

· Y P3_9, X Sex

· Same test as 7, Evaluate

9) In a separate survey I found that Women were more ‘Pro-Choice’ than men and that Catholic women were significantly ‘More, more Pro-Choice’ than Catholic men. Is this true of the respondents to this survey? How did you test that? If you did find the gap between Catholic men and women significantly greater than the gap between men and women in general what would a statistician call such a phenomena? If it were true, how would you explain it?

1) Use same data table as questions 7 and 8

2) Create a subset

· Rows---Row selection---Select where---A selection box appears---Select Religion, equals, and type catholic (ie choice 2)

· Select table—subset, Name table

· Open new subset table

· Fit Y by X

· Same analysis as Questions 7 and 8

10) Are republicans different than non-republicans on the responses to any of the questions about immigration?

1) Create a republican/non-republican column

· Cols—New Column, name column, change data type to numeric and nominal

· Cols—Formula

· Type formula: If Polprty = =2 “R” else “N”

2) Analyze using new column

· Fit Y by X

· Y = P4_B1-5, X = new column

· Same tests as 7,8,9

11) Is there any relationship between ‘Religiosity’ and responses to the question: ‘The earth has a finite supply of natural resources such as water, arable land, etc. which imposes a limit on the number of people which can sustainabily live on it.’

· Change ReligACT to continuous data

· Fit Y by X

· Y = P1_15, X = ReligACT

· Select Fit line test

· Evaluate test

Factor Analysis (12-14). Factor analysis is a data reduction technique that allows you to ‘compress’ your analysis. As you can imagine we could ask hundreds, if not thousands of questions of this dataset (e.g. are men different than women on questions 1-50, are catholics different than protestants on questions 1-50, there’s a hundred right there). However, as you can imagine, people will have similar responses to many of the questions. Factor analysis allows you to capture the co-variance that usually exists between questions. For example, there are 5 questions about immigration or immigration policy; an anti-immigration person will most likely respond in a similar manner to all the questions and only one question is often necessary to ‘capture’ such a response. Factor analysis is a means of ‘capturing’ this co-variance between questions and ‘reducing’ a many-question survey to a few factors. Labeling or ‘Naming’ these factors is one of the ‘arts’ of statisticians. It is now your turn to practice this ‘art’.

12) Run a factor analysis on the responses to the questions appropriate to such an analysis (we’ll decide these in class). Identify the questions with a factor contribution score of 0.40 or more for each factor and list the questions associated with factors 1-5. Be sure to save each respondent’s factor scores on each of Factors 1-5. For Factors 1-5 list the questions with a factor contribution score of 0.40 or more and study the questions that contributed to each factor. As a result of this study provide a name for each of the first five factors. (FYI, potential ‘names’ for factors when I analyzed this survey were: “Faith in Government”, “Belief in Adam Smith’s ‘invisible hand’”, and “Keep those Mexicans out of California”). Try to come up with your own (it’s actually kind of fun J).

1) Clean up data

· Select question columns P4_A, delete

2) Perform Multivariate Correlation

· Analysis—Multivariate

· Ycolumns = All survey questions (Shift key to select multiple items)

· Select test (red triangle), principal components—correlations

· Select red triangle next to Principal Components/Factor Analysis—Factor Rotation—type 5 for factors---click ok

· Save Rotated Factors

· Evaluate factors for significance, i.e. questions with > 0.4000 value for factor 1-5

· Name your factors by the types of questions that are significant

13) Do all the statistical tests necessary to fill out the table below. Put an asterisk (*) in the cells that indicate any significant differences on factor scores between demographic varibales. For each asterisk provide a detailed description of the nature of the significant differences and some guess as to an explanation for the differences. Your ‘guess’ is referred to as ‘theory’ in academia. If you are really fired up about this exercise find references to support your theory.

Significant Factor Score Differences (*)	Sex	Pol. Party	Religion	Religiosity	Income	Education	Race/Ethnicity
Factor1:
Factor 2:
Factor3:
Factor4:
Factor5:

· Carry on from Question 12

· Fit Y by X, Y = sex (first category in table above) X = factor 1-5

· Select Means/Anova/t test

· Repeat fit Y by X for each category in table (polparty, Religion etc)

· Place asterisk in table for categories that are statistically significant

· Evaluate all test results for goodness of fit of factor and category

14) Did filling out the table and answering the questions of #13 make you appreciate factor analysis? (Explain. If your answer is ‘No’ stop by my office for a spanking J).

· Please BS an answer here that won’t get you a spanking

Spatial Anaysis: Where’s the Geography?

So far, the analyses performed up to this point could have been done in a sociology department. The only ‘geographic’ analyses were the questions about randomness of the survey respondents with respect to population density and space. True spatial anlysis of surveys can shed light on interesting questions about the location of the respondent’s home or workplace relative to questions in the survey. For example: Does the distance of a respondent’s home and/or work location influence their likelihood to support or use a light rail public transportation system? Does the population density of their home location or home city covary with attitudes about population growth and policy? Does the Hispanic proportion of their home neighborhood have any influence on their attitudes about U.S. immigration policy?

15)Test for any significant differences/variation for all of the factor scores (1-5) and the population density and percent non-white of the respondents home location. If you find any significant differences provide an explanation?

1) Export JMP file: Save JMP file as a text file (.txt) file with factor columns 1-5

2) Import to excel, open text file as comma delimited

3) Prepare data for Geocoding in Excel

· Open—files of type--txt—select exported JMP file--click ok

· A dialog box opens, select delimited, click next, select comma, next, finish

· Create an new column in the data table called intersection

· Higlight new column, click on = in formula bar, in function pull down menu on formula bar select more functions and select concatenate

· In Concatenate dialogue box: click on text1 text box, scroll over and select HmStrt_ column, click on text2, type “ & “, click on text3, select Hmxstrt_ column, click OK

· Fill down on new column

· Save as: dbfIV format

4) Geocode in ArcView

· Open ArcView, add new dbfIV table,

· Open a new View, add theme sbcoblocksdemog.shp, add streets layer, add surveyresultswithgeojoin layer, add surveylocneq483

· Turn on Geocoding

o Make streets active theme

o Theme—Properties—Geocode—US Streets

· View—Geocode address: See figure 1 for values

o Click on Geocoding preferences, lower thresholds to 5

o Click Batch Match

o At Partial Match error, select partial match

o Do interactive match

o Correct errors (this sucks, Congrats! you are a Graduate student)

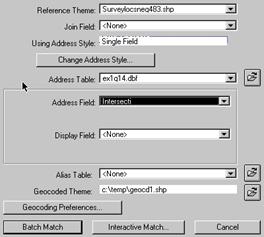Figure 1: Geocode address dialog box (From view pulldown menu)

5) Join geocoding with survey data

· Open imported excel table, open blocks table

· Join excel table to blocks by shape field

· Export joined table as a text comma delimited format

6) Analyze data in JMP with respect to spatial location

· Open JMP, open data file, select correct file format and ArcView exported table

· Analysis, Fit Y by X, Y = Factors 1-5, X = Pop density

· Perform Fit line test

· Evaluate results

· Repeat JMP analysis with X = white/non-white

15) Another test you could do is to test for increases variance in response based on a geographic attribute. For example, suppose that people’s responses to the 5 immigration questions became increasingly extreme (i.e. more 1’s (strongly agree) and 5’s(strongly disagree)) but the mean remained the same as the Hispainic proportion of the population in the respondent’s home location increased. What kind of statistical test would you use to look for that and if it proved significant, what would the explanation be?

Hint: What statistical test compares variances?

General Questions

16) Describe 10 specific problems related to this little research project. Things to consider: Sampling frame was registered voters whereas census data was total population, Non-response Bias, etc.

17)Are these problems significant enough to invalidate any or all of the findings from an analysis of this data?