Jane Doe Spatial Stats 3650 2001 DU

Lab Exercise #2: Correlation, Regression and Modeling of Population and Population Density with nighttime imagery provided by the DMSP OLS satellite.

In this lab you will perform analyses and use data associated with my dissertation: Census From Heaven: estimation of human population parameters using Nighttime Satellite Imagery. The datasets are of the world, United States, and Los Angeles basin.

Outline of your tasks/objectives

First you will look at the global datasets are try to build a model that estimates the population of the cities based only on manipulations of the nighttime image. Then you will try to improve that model by incorporating aggregate national statistics.

Second you will apply a similar model to the U.S. data and note the differences in performance and provide and explanation for such. Then you will look at the U.S. data to develop a disaggregate population density model based in some way on the spatial nature of the data or the intensity of the light.

Thirdly you will look at the concept of ‘ambient’ population density in the Los Angeles area using both residence and employment based population density.

Finally you will select some city in the U.S., build a population density model for it using the nighttime imagery, map the residuals in your model and produce a publication quality one-page figure characterizing the model and its performance for you particular city.

Analysis of World data

Task #1: Using Arc/INFO and/or ArcView create a polygon coverage that has every contiguous blob of light in the nighttime image (to do this you will need to create a binary grid from the ‘earthatnight’ grid using the CON function in grid). Next you will have to do a REGIONGROUP command in grid. Next a GRIDPOLY command so you have a coverage of polygons that represent all the urban clusters in the world as identified by the nighttime imagery. Each of these polygons has a unique ID.

Task #2: You will need polygon coverage to have the following attributes: AREA, COUNTRY (preferably a FIPS code), GDP/Capita of Country, # of cities with known population that fall inside polygon, the names of these cities as one long string, and the sum of the population of these cities. (sometimes due to conurbation more than one city falls into these polygons

DFW

)

Task #3: Output this table into a txt or dbf file that can be read into MS Excel. Export it from Excel as a tab delimited text file and read into the JMP statstics package.

Answer the following questions:

1) 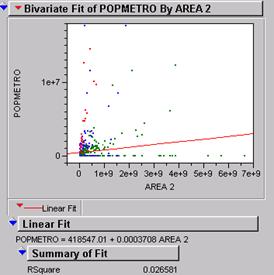Run a simple linear regression between area and total population in the table. Describe the results and problems:
This illustration of the best fit line is not very good with a r² of .026. With 743 records it is highly likely that any best fit would be significant even though it may not be representative. In this case the few outliers (big cities) are influencing the relationship while the large majority of records are globbed up near the lower limit of the range.

2) 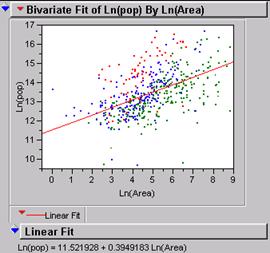Transform your area and total population values to Ln(Area) and Ln(total population) and run the regression again. Describe the results and problems.
Taking the log of both variables spreads the data over an area that can be more accurately analyzed for their relationship. The r² is up to .36 and even though that is not great it is a big improvement.
Ln(pop) = 11.52 + .3949 * ln(area)

3) Color code your points so that points representing cities in countries with a GDP/capita less than $1,000 / year are red, $1,001-$5,000/year are blue, and over $5,000/year are green. Run the same regression on Ln(area) vs. Ln(total Population). Describe the results.
The high income group has a lower intercept and a more level slope.
Ln(pop) = 10.70 + .475 * ln(area). r² = .44
The middle income group has a higher intercept and a similar slope.
Ln(pop) = 11.09 + .519 * ln(area). r² = .38
The low income group has a similar intercept and a steeper slope.
Ln(pop) = 11.67 + .623 * ln(area). r² = .32

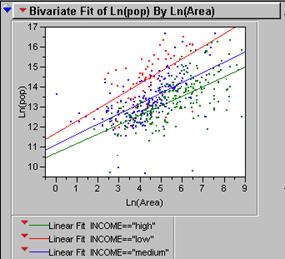
This indicates that as a city gets bigger the number of wealthy people increases at a lower rate than the number of people with very little money. LDCs may be under-estimated.

4) Create a new column in JMP called IncomeClass or something based on the red, blue, green code above. Run separate regressions on ln(area) vs. Ln(total population) for each class. How do these regressions on subsets of the data compare to the regression on all the data. Describe and explain the difference.
See above explanation.

5) Assume you only had the regression knowledge from the previous exercises and you had to estimate the populations of Mumbai (Bombay), India; London, England, and Cali, Colombia from only their areal extent as measured in the nighttime satellite image. What would your estimates and 95% confidence intervals be for those cities if you used the global parameters? What would your estimates and 95% confidence intervals be for those cities if you used the regression parameters derived after sub-setting the data to ‘rich’, ‘mid-income’ and ‘poor’? Check the “actual” population figures for those cities and see if they landed inside your 95% confidence intervals.
You would insert the area in the equation to solve it for population.
Ln(pop) = 11.52 + .3949 * ln(area)

London: ln(pop) = 7.0892 So, 11.52 + .3949(7.0892)

Est = 1,658,791 Actual = 7,015,781

Cali: ln(pop) = 5.1475 So, 11.52 + .3949(5.1475)

Est = 770,479 Actual = 1,832,321
Mumbai: ln(pop) = 6.0331 So, 11.52 + .3949(6.0331)

Est = 1,093,074 Actual = 14,482,636

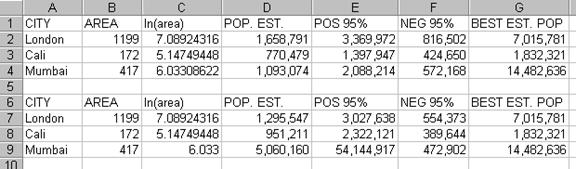
To find the 95% confidence interval for these estimates you must multiply the standard error of the intercept by the z-score of alpha = .05% which is 1.96. or read same off jump printout. To get the upper limit you add this number to the variable in the equation and to get the lower limit you subtract it. Do the same for the slope. Do both upper and lower limit for each of the three cities. See table above.
The London estimate is lower than the actual population of London because they have restricted use of nighttime lighting as a matter of policy. Probably a postwar response to the blitzkrieg. Cali and Mumbai are with in the confidence range established by the equation.

6) How could you use these regression models, a nighttime image of the world, and a % urban figure for every nation of the world to estimate the total global population? From the nighttime image you can identify all the urban centers in a country. From the regression equation (using the log of area and log of population) you can determine parameters and make an estimate for each of the urban centers. The sum of those population centers is the total urban population of a country. Once you know the % urban then you can calculate the total population of each country. For example, if the sum of urban residents is 4million and the per cent of the total population that is urban equals 80%, then the total population of the country is 5 million people. ‘Lather Rinse Repeat’ for every country to get the global population.

Analysis of United States Data

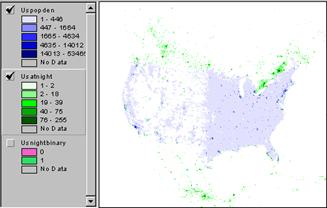
Task #1: Generate a table similar to the one you did for the world using the population density and nighttime imagery grids for the United States.

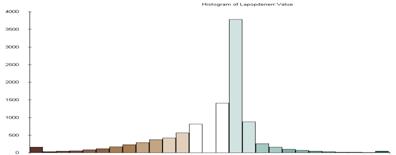
7) Produce a histogram of the population density data.

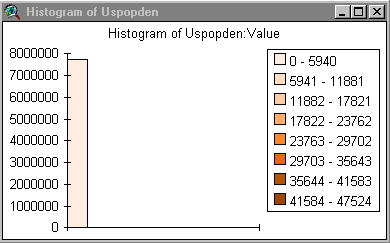
8) Produce a histogram of the usatnight data.

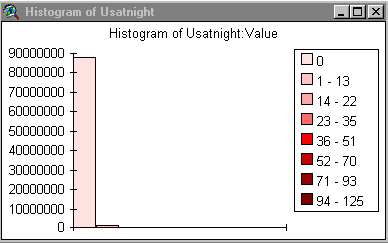
9) By looking at these histograms comment on the likelihood that a model derived from nighttime light emissions could predict population density.

The histograms look similar so you would think that it might work pretty well.

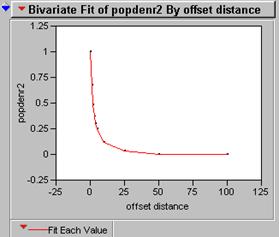
10) Produce a correlogram of the pop density data (use the CORRELATION function several times)

11) Produce a correlogram of the usatnight data

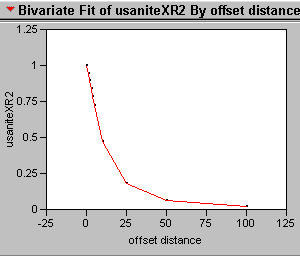
12) What does the correlogram of the popdensity data suggest about the effectiveness of a perfect model if it is mis-registered by one pixel?

The first pixel costs the greatest amount of correlation. The second one is worse but not twice as bad. How can this be, when we know that the greatest chance of two things being exactly alike is related to their proximity? The answer is that autocorrelation causes an inflated r2 inside the lag zone. The correlogram indicates by the steepness of the curve something about the randomness of the data and the edginess of the clusters.

If you think about the correlation of the binary mask image then you can imagine that the cluster of 1slands mostly on 1s when the shift is just one pixel. In fact only the edges of the cluster will be landing on the 0s that are outside the cluster. Big solid clusters will have flat smooth correlograms while tiny clusters that have more edges than central pixels will have sharp steep correlograms.

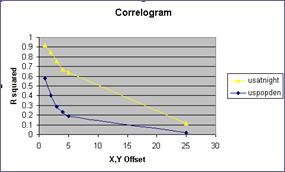
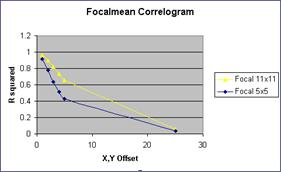13) Run a FOCALMEAN on the pop density data? (use a 5x5 and an 11 x 11 filter). Now generate two new correlograms for the ‘smoothed’ data. How does FOCALMEAN work, and how does it change the data?

The focalmean works like a convolution window where the average of the nearest neighbors is placed in the center square for each cell in the data set. This function smoothes the data. The bigger the window, the smoother the data. The correlograms are not as steep after the data has been smoothed.

Smoothing the data from the popdensity brings the correlogram into line with the usatnight. Once the data has been normalized in this way the regression equation should be more accurate.

14 ) Perform the same Ln(area) vs. Ln(Population) regression on this data.

Where is smoothed data grid from focalmean and where does us binary grid fit into the discussion.?

World : r2 = .261

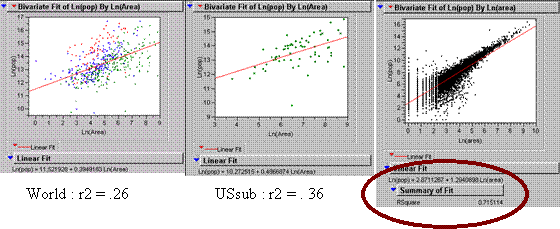
How is it different than the results for the U.S. from the world-level analysis? Describe these results and the differences from the U.S. results in the world-level analysis. Which regression parameters do you think are more accurate? Does this U.S. level study weaken or strengthen the argument that the areal extent of a city as measured by the DMSP OLS satellite is a good predictor of that city’s population?

The big increase in the r2 for US data is due the fabulous quality of the US census data. Finer scale resolution and better data quality actually make the relationship stronger with an r2 of .715. This could be interpreted as a verification of the method since the regression line has a better fit when better data is used to build it.

15) Use the CORRELATION command in grid to get a simple correlation coefficient between the U.S. population density grid and the usatnight grid. Record this R or R². Comment on its value and provide an explanation. The r2 in this correlation is 0.24 and that is not the best thing to hang your hat on. People sometimes turn off the lights where they live at night. Often they put up lights where they need to be at night. Roads, parking, and entertainment areas are all brightly lit at night.

16) Model Building: We have just evaluated a simple model to predict population density from nighttime image. The model was a simple linear model that suggests that light intensity as measured by the DMSP OLS is directly proportional to population density. Our R² was not 1.0 so our model was not perfect. Build a better model, describe/define it, justify it, and evaluate it. Describe how it compares to the simple aforementioned model.

We have identified several other factors that account for errors in these models. A weighted multivariate relationship probably exists in which several elements of the landscape are working together to determine the actual population of a city. High density is not a random act of God. People choose to live close together (or far apart) for reasons that are emotional, practical, economical, political, physical or any combination of those factors. Then they put up lights to indicate where they spend the most time at night, which is not necessarily where they live.

Analysis of the Los Angeles Data

Characterize ‘ambient’ population density as a temporally averaged measure of population density that accounts for human mobility, employment, entertainment, etc.

17) Apply your model of population density prediction from before to the Los Angeles urban cluster.

a) What is the correlation of your model to residence based pop den?

R = .46

b) What is the correlation of your model to employment based pop den?

R = .35

c) What is the correlation of your model to the average of these two?

R = .56

18) What do your results above suggest regarding your model’s ability to predict ‘ambient’ population density? Taking the average of the pop density and the job density give a better picture of where people are, so the lights seem to indicate a stronger relationship with where people are than they do with where people sleep.

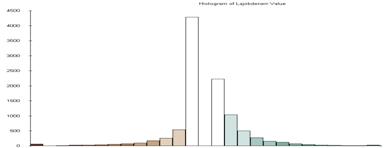
19) Visualization of Error: Subtract your model from each of the following: Residence-based pop den, Employment based pop den, and average of Residence and employment based pop den. Which errors look most random? Which ‘map of residuals’ has the smallest mean absolute deviation?

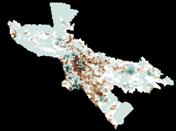
These histograms of the error between the model and the three data sets that were used to create the model show that the estimate works pretty well for the ambient population. Night lights (rad cal) is a good indicator of where people are at night, if you do not assume that they are all at home.

LAjoberror

LApoperror

LA error

Some interesting things about the residual maps and their histograms. The mean of the error is not always the value 0. Green indicates the places where the estimate is too high, while the brown show where the estimate is too low. The size of the standard deviation used for the classification of course is based on the range of values and the variance so it is also different for each map.

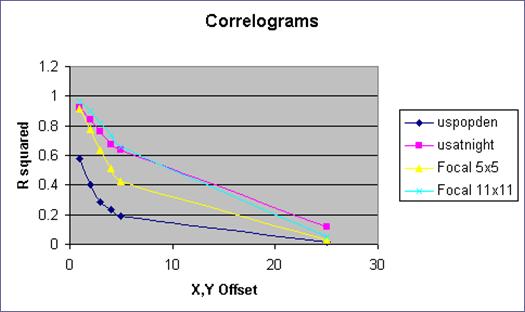
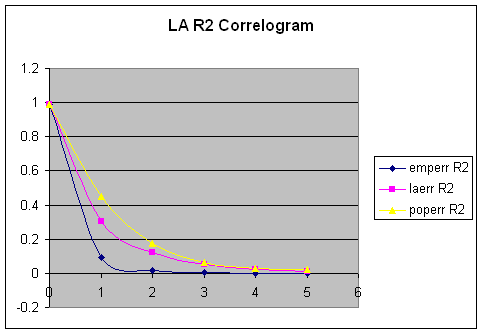
Produce correlograms for each of these residual maps. What do these correlograms suggest about these three images?

Offset	emperr	laerr	poperr	emperr R2	laerr R2	poperr R2
1	0.304	0.5514	0.6731	0.092416	0.30404196	0.45306361
2	0.1369	0.3509	0.4176	0.01874161	0.12313081	0.17438976
3	0.0791	0.2283	0.2525	0.00625681	0.05212089	0.06375625
4	0.0053	0.1445	0.1764	0.00002809	0.02088025	0.03111696
5	-0.0061	0.0952	0.159	0.00003721	0.00906304	0.025281

Study your own city

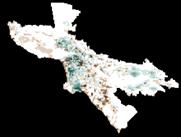
Apply your best population density model to Dallas Ft. Worth and evaluate the model. Get a map off the web. Generate a map of your errors or residuals. Produce a one-page publication quality figure showing this city, your model, the errors, the nighttime lights image, and a map of the city. Explain model and errors as briefly as possible.

See attached graphics. When the popdensity map is subtracted from the estimate, the result will be positive in every cell that was over estimated. Over estimated areas tend to be brightly lit locations where people go at night rather than where they live. Under estimated places ( negative errors) are those that have very high density because an apartment building for 150 residents may have the same amount of lighting as one for 1500 people.

I looked at DFW. A twin city metro-plex with an enormous airport in the center. The graphic shows the night light image, the population density, and the relationship between them as a regression line equation. The population estimate is made from the nite lights using the equation, then the actual population density map is subtracted from the estimate to show where the error occurred.

The histogram of the error is not symmetrical. More cells are under-estimated than over estimated and yet there is a spike at <3 Std D where really high density areas were really way off. It is possible that there is not a similar spike on the opposite end of the histogram because the image mask was clipped at the low end of luminosity.