Jane Doe

GEOG3560

Lab Exercise #2

April 29, 2001

Analysis of World Data

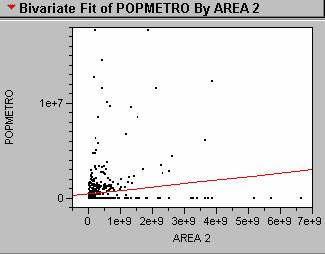
1. The regression line generated from the world cities data is shown below.

Population = 42060 + 0.00018(Area)

The R2 for the regression line was 0.0184, and the p value was significant at less than 0.0001. As you can see in the scatterplot shown below the majority of the world’s cities are smaller and so many points cluster near the origin of the plot. The data does not seem to show a linear relationship, in fact the data points appear to increase exponentially as the area increases. Also, there are numerous points where an area was defined, but population data was not available. To perform the regression I used POPMETRO instead of POPPROPER for my population variable. The clusters of light identified for each city would most likely include all of the surrounding suburbs around the city itself. So, the metro population count would be a closer approximation to the actual population included in each cluster. Unfortunately, since the R2 for the regression line is 0.0266 only 2.66% of the variation in the data is explained by the model. This model is not a good approximation of the relationship between the area of nighttime imagery clusters and population.

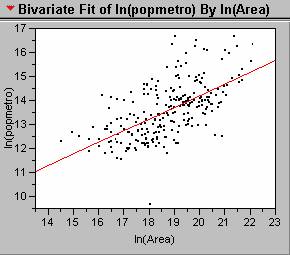
2. Transforming the data by taking the natural log of both the area and population improves the linear relationship between the variables, and results in a better regression model. The regression equation for the transformed data is shown below.

Ln(Population) = 3.60 + 0.524[ln(Area)] ;

Looking at the scatterplot shown below, there is a marked inprovement over the simple linear regression from question 1. The outlier near the lower axis is Valetta, Malta, and the some of the outliers near the top edge of the graph are Mexico City, Calcutta, and Bombay. The R2 for this equation is 0.367 with a significant p value of less than 0.0001. Still only 36.7% of the variation in the data is accounted for using this model, so there must be some other variables influencing the relationship between the area of nighttime imagery clusters and population.

3. Color coding the city data by GDP/capita, generated the scatterplot shown below.

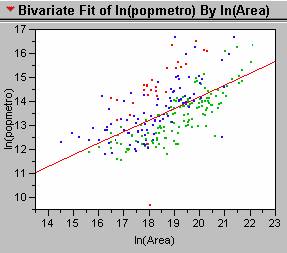
There certainly appears to be a pattern in the distribution of points for the different income classes. The red dots, representing countries with GDP/capita of less than 1,000 appear above the regression line. In these countries the model underestimates the true population. This makes sense since the less developed countries would have less nighttime light output per person. Conversely, the model overestimates the population for the richest countries, represented by the green dots, since their nighttime light output would be greater per person than in the less developed countries.

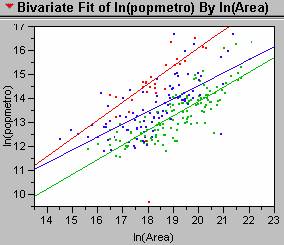
4. The new regression lines generated for each of the three income classes are shown in the scatterplot below. The equation for the red line representing those countries with a GDP/capita of less that 1,000 is:

Ln(Population) = -0.716 + 0.837[ln(Area)] ; R2 = 0.767 ; p value <0.001

For those countries with GDP/capita between 1,000 and 5,000, the regression equation is:

Ln(Population) = 2.200 + 0.612[ln(Area)] ; R2 = 0.507 ; p value <0.001

And for those coutries with a GDP/capita greater than 5,000, the regression equation is:

Ln(Population) = 0.876 + 0.643[ln(Area)] ; R2 = 0.709 ; p value <0.001

These individual regression models based on income class all have larger R2 values than the original aggregated model. Income class is definitely a confounding variable when trying to approximate population of cities based on nighttime imagery data. So, it may be more accurate to identify the income class for a city and then to use the appropriate regression equation to approximate its population.

5. I wasn’t able to find any data for Mumbai, so I selected another Indian city with a low income class, Chandigarh.

Global Parameters

Chandigarh, India: PopEst=416,304 ; 95% C.I.[21,880 to 8,144,232]

Cali, Columbia: PopEst=812,382 ; 95% C.I.[38,554 to 17,623,118]

London, England: PopEst=2,300,430; 95% C.I.[100,973 to 33,423,871]

Income Classed Regression Parameters

Chandigarh, India: PopEst=1,471,393, 95% C.I.[1,227 to 1,706,190,689]

Cali, Columbia: PopEst=1,075,625 ; 95% C.I.[13,172 to 89,707,185]

London, England: PopEst=1,855,633 ; 95% C.I.[100,973 to 33,423,871]

The populations for Chandigahr, Cali, and London were given 662,064 ; 1,832,321 ; and 7,015,781. These “actual” populations did occur within the confidence intervals defined for all of the individual predictions. The confidence intervals for the income classed regression lines are much larger then those for the global regression. Classing into income groups divides the data into 3 groups, reducing the number of observations used in each regression. With this decrease in sample size the variability in the data increases, and the confidence intervals become larger.

6. Estimating the total global population using just the regression equations from above, a nighttime image of the world and a % urban figure for each nation, would involve several steps. First, the nighttime image would have to be processed in Arc. You would need to 1) create a binary grid of the data at a specified light level threshold, 2) identify each light blob or cluster of light, and 3) calculate the areas for each of the clusters (sum of the number of pixels). Then using the regression equation for the global data, calculate a population estimate for each cluster. Assuming that you have access to the GDP/capita data by country, you could select the appropriate regression equation to use by income class. The output of the regression equation gives an estimate of the urban population (UrbanPopest). The total population is the urban population plus the rural population. To calculate a Population estimate for each cluster you would use the following equation:

Populationest = UrbanPopest / %Urban

After all the Population estimates have been calculated, then they can be summed to estimate the total global population.

Analysis of United States Data

7. Histogram of Population Density 8. Histogram of Usatnight

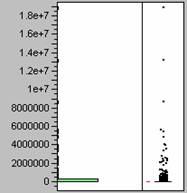
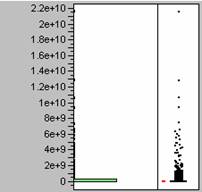
9. The histograms show that the population density data and the nighttime light emissions data are similarly distributed. Both sets of data are heavily weighted towards the lower numbers, or positively skewed. Because the two sets of data have similar distributions it does seems probable that one could be used in a model to predict the other.

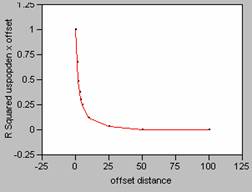
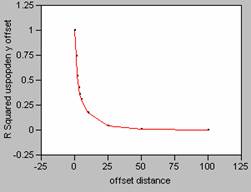
10. Correlograms for Population Density

Offset in the X Direction Offset in the Y Direction

11. Correlograms for Nighttime Light Emissions

Offset in the X Direction Offset in the Y Direction

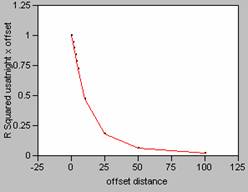
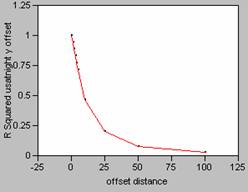
12. The correlograms show that as the offset distance increases, the correlation as measured by R2, decays rapidly. If a perfect model (R2 = 1) is mis-registered by one pixel, it will decrease the effectiveness of the model. When a correlation was run on uspopden to itself, using an offset of 1, the r value dropped from 1 to 0.8203 (x offset) and 0.8623 (y offset), dropping the correlation coefficient value by approximately 18 and 14%. Mis-registering a model by an offset larger than one pixel would result in even greater changes until the offset reaches about 25, then there wouldn’t be very much correlation between the variables of the model at all.

13. Correlograms for Population Density smoothed with a 5 x 5 filter

Offset in the X Direction Offset in the Y Direction

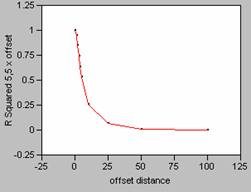
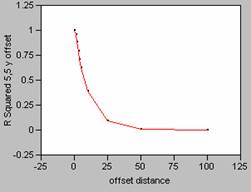
Correlograms for Population Density smoothed with an 11 x 11 filter

Offset in the X Direction Offset in the Y Direction

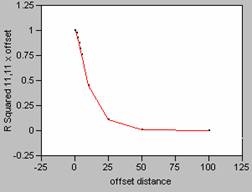
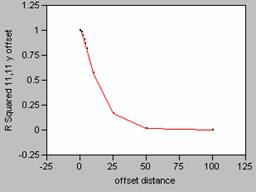
The FOCALMEAN command in Grid, averages the values found within the window (in this case 5 x 5 or 11 x 11), and then stores that average value at the location of the central cell of the window in a new grid. This effectively smoothes the data since the average calculation takes out the highs and lows in the data. As the size of the window of the filter increases, more data is taken into account in calculating the average causing the data to be smoothed even more. As the data is smoothed it also alters the shape of the correlogram curve changes, causing it to drop off far less rapidly. This makes sense intuitively since there would be less effect in mis-registering data with less variability.

14. The regression analysis using the United States data set yields the following regression equation:

ln(population) = -15.01 + 1.29[ln(area)] ; R2 = 0.715 with a p-value of

less than 0.0001.

The scatterplot and regression line are shown below.

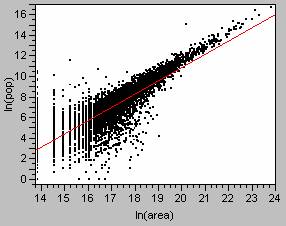
The U.S. data set was in the form of a grid with a population density value for every 1 km2 in the U.S. For each cluster of light identified, the same cluster of pixels were identified in the population density grid and then summed to get a population estimate. Using a population density grid covering the entire United States ensured that there was population data for each and every cluster, increasing the number of data points used in the regression analysis. There were 6566 data points used in the U.S. data set regression analysis.

A different method was used for the world data set analysis. For the world data, each cluster of light was identified with the location of a city. Then the population data for the city could be associated with the cluster. Unfortunately, many of the cities didn’t report a population, or reported only a population proper value, when a population for the surrounding metropolitan area would have been a more accurate assessment of the true population. For my analysis of the world, data from 832 cities were used to generate the regression model. By selecting just the U.S. cities from the data for the world (cutting the number of observations to 85), another regression analysis was done resulting in the following equation:

ln(population) = -3.38 + 0.848[ln(area)] ; R2 = 0.710 with a p-value of

less than 0.0000.

The scatterplot and regression line for the analysis are shown below.

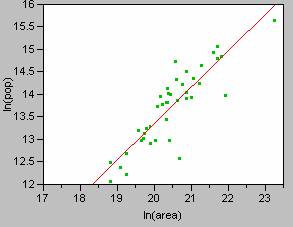
I believe that the regression parameters calculated using the U.S. data set are more accurate. The 70 fold increase in the number of points used in the regression has to make a difference in the accuracy of the equation parameters. It is interesting to note that although a completely different line is described for each of the equations, the R2 value for each regression is very nearly the same. The U.S. study doesn’t weaken the hypothesis that the areal extent of a city is a good predictor of population, it strengthens it. The U.S. study uses a more detailed method to measure the population within each cluster (the population density grid) and comes up with a similar relationship, which in effect verifies the results of the world study.

15. The correlation coefficient between the uspopden grid and the usatnight grid was 0.4919. The positive coefficient implies that there is a positive correlation between population density and the nighttime emission levels, so as one increases the other will also increase. Whether a correlation coefficient is significant is dependent on the sample size. Since these grids contain a lot of data, and R is dependent on sample size, the magnitude of the correlation coefficient does not provide much information. For more information about the relationships between two variables a regression analysis is typically run.

16. Looking at the scatterplot for the first U.S. regression described above, it is interesting to note that the regression line deviates from the observations as the ln(pop) and ln(area) increase. The regression line would underestimate the populations for the largest of U.S. cities. The observations from the smaller cities effectively pull the regression line down because there are far more small sized cities in the U.S. than large ones. One method to counteract this effect is to weigh the observations by the population, in this way the data from the larger cities is given more precedence. Another analysis was done, this time weighing the regression by the count, the number of pixels per cluster. The regression equation and scatterplot with regression line are shown below.

ln(population) = -18.40 + 1.489[ln(area)] ; R2 = 0.9500 with a p-value of

less than 0.0000.

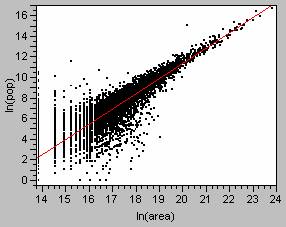
This weighted regression model has a higher R2 value, this model accounts for 95% of the variation in the data. Looking at the scatterplot, you can see how much better the line hugs the observation points.

Analysis of the Los Angeles Data

17. To create a model of population density prediction for Los Angles, I used Arc to create a table containing the grid values for lanightradcal, lapopdensity, lajobdensity. This table was exported into JMP and regression analyses were run on the data. The regression results are show below.

Regression Model for Population Density vs. Nighttime Light Emissions

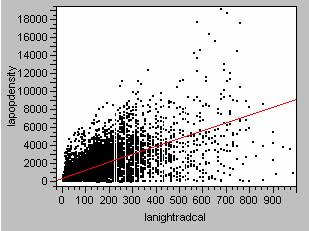
lapopdensity = 431.39 + 8.77lanightradcal ; R2=0.441 ; p value<0.0000

Regression Model for Employment Density vs. Nighttime Light Emissions

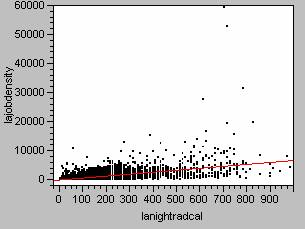
lajobdensity = -50.23 + 6.73lanightradcal ; R2=0.340 ; p value<0.0000

Regression Model for Ambient Population Density vs. Nighttime Light Emissions

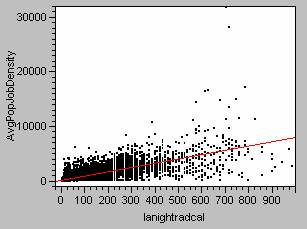
AvgPopJobDensity = 190.58 + 7.75lanightradcal ; R2=0.54 ; p value<0.0000

To create a population density estimate for Los Angeles I used the population density regression equation to generate a new grid of the population density estimate. My population density estimate grid was used to calculate the following correlation coefficients.

a) Correlation between my population density estimate and the residence based population density, 0.5397.

b) Correlation between my population density estimate and the employment based population density, 0.4693

c) Correlation between my population density estimate and the average of the two, 0.5932.

18. The correlation between the grids suggests that the average of the residence and employment based population densities would give the best results when attempting to define a model between nighttime light levels and population. This average would take into account the illumination from residential areas plus the lights from any large industrial or commercial areas. Using this measure of ambient population density will hopefully result in a model with greater accuracy in predicting populations from nighttime light emissions.

19. I created a new grid using the ambient population density regression equation and then created the error grids shown below. The data is displayed in standard deviations to allow for comparisons between the maps.

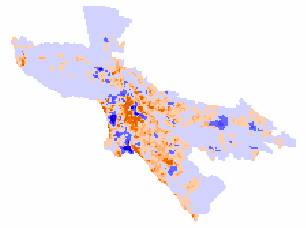
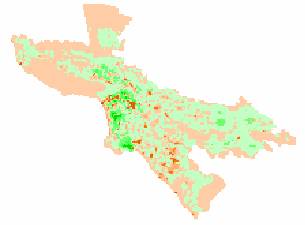
Population Density – Ambient Population Density Estimate

Employment Density - Ambient Population Density Estimate

Ambient Population Density – Ambient Population Density Estimate

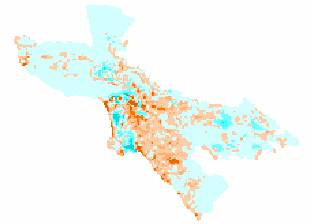
Reviewing the maps, the patterns of error appear to be very similar between the population density error map and the ambient population density error map. The central areas are underestimated (oranges), since the positive error means that the model values are smaller. The outskirts of the city are overestimated on both of these maps (negative errors – in blue and cyan). Far more areas on the maps are overestimated than underestimated (more blue and cyan than orange). The pockets that are highly overestimated (dark blue and dark cyan) occur in the same locations on the two maps. So it appears that the locations of these errors are not random and possibly are caused by autocorrelation between the data sets. The patterns on the job density error map are different. There are more areas in the orange tones, indicating that the model underestimates the job density throughout much of the map. Some of the same pockets of heavily underestimated areas (darker green) occur in the same locations and patterns as the other two error maps. I’d have to say that the job density map seems to be the most random, since its error patterns are different from the other two.

To find the smallest mean absolute deviation, the absolute values of the grids were calculated using Arc. Using Arc’s Describe function the means of the absolute value grids were found. The means for the three maps were:

Population Density Error - |mean| = 746.98

Job Density Error - |mean| = 611.281

Ambient Density Error - |mean| = 496.07

The smallest of these values is the |mean| for the ambient density error map.

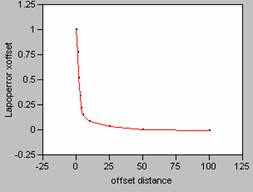
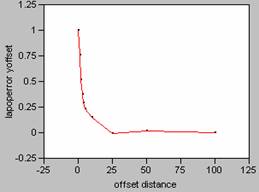
Correlogram for LA Population Density Error

X offset Y offset

Correlogram for LA Employment Density Error

X offset Y offset

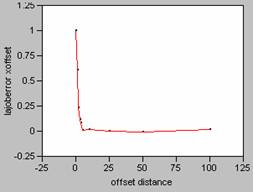
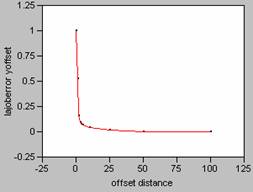
Correlogram for LA Average Population and Employment Density Error

X offset Y offset

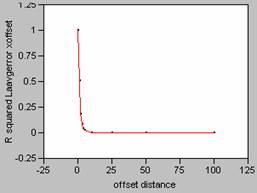
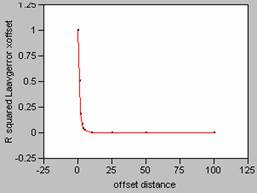
Plotting the correlograms for the three error maps for x and y offset simultaneously yields the following graphs.

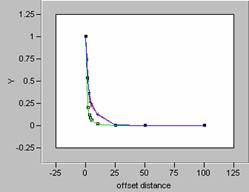
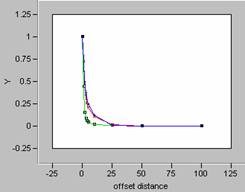
In the Focal Mean question done earlier in this lab, the correlograms of the smoothed data showed a marked softening of the decay pattern for the curve. So, the more variability in the data, the sharper the decay pattern shown in the correlogram. For the three error maps calculated for this data set, the curves for the job density error map have the sharpest decay patterns, and so, the job density error map contains the most variability. Increased variability on an error map would indicate more random errors. This supports the discussion of which map was more random from earlier in this question. Visually the job density error map appeared to be the most random, and that has been confirmed by reviewing the shape of the correlogram curves. It is interesting to note that the correlogram curves for the other two error maps, population density and ambient density plot almost as one curve, an indication of how truly similar those two maps are.