John Doe

 

GEOG 3650 – Spatial Statistics

 

 

Lab #2 – Correlation, Regression, and Modeling of Population and Population Density with Nighttime Imagery Provided by the DMSP OLS Satellite

 

 

ANALYSIS OF WORLD DATA

 

 

Procedure:   (using ArcView Spatial Analyst)

 

a.       Select earthatnight grid and set pixel threshold to 36 using map calculator to isolate smaller light patches from significant urban centers.

b.      Convert threshold output to grid and then convert to shapefile to get numbered polygons with unique ids.

c.       Run calculate.feature.geometry script to obtain areas and perimeters of polygons in cluster table.  You will have to cut and paste this script into the script window using Notepad.  Compile and Run the script.

d.      Do a spatial join (can use Geoprocessing Wizard) between Wrldcluspoly table and Worldcities cover.  This aggregates cities with correct polygons and provides a table with some of the required city information such as population, country fips code, etc.

e.       Import NationalPopIncomeUrbanData table into ArcView as a .dbf conversion from Excel.  This table contains the required GDP/Capita table and a field with fips_cntry code.

f.        Join the NationalPopIncomeUrbanData table to the Worldcities table on the fips_cntry.  Join  Worldclusterid table with counts and values on the value field to the wrldcluspoly_id field in the Worldcities table..  You now have cluster counts, city names, GDP/Capita, and population figures in a single table.  Export this table from ArcView as a .dbf file and bring it into JMP as a MSDOS text file for the rest of the statistical analyses.

 

1)  Run a simple linear regression between area and total population for each of the cities in the table.  Describe the results and problems.

 

First, be sure to clean up the imported JMP table.  I removed all rows with no valid Area2 or PopMetro data.  Even when this is done you will find countries with no GDP/capita data.  World data is not as complete or as accurate as data for individual countries because of the vary levels of census quality.

 

 

 

 

 

 

 

 

 

 

 

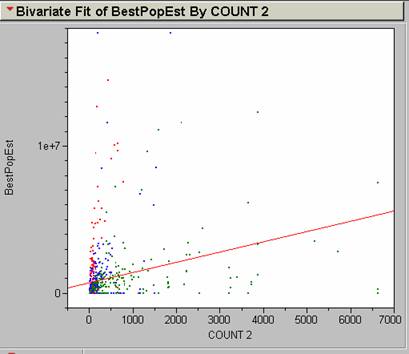
Run the regression using Analyze ŕ Y x X Fit.  Put Count2 on the X axis (independent variable) and BestPopEst on the Y axis (dependent variable).  The correlation and best R2 values show no significant relationship.  R2  = .071205.  There are a lot of outliers that affect the position of the regression line.

 

 

 

2)  Transform your area and total population values to Ln(Count2) and Ln(BestPopEst)  and run the regression again.  Describe the results and problems. 

 

            Make new columns for the new variable and populate them with the formula editor, then run the Y x X fit.

 

 

 

 

 

 

 

 

 

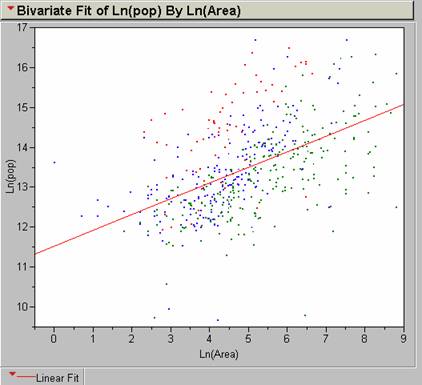
      A much better correlation exists for the transformed values.  R2  = .26119 with an n = 498.  This is a weak positive correlation. 

 

 

 

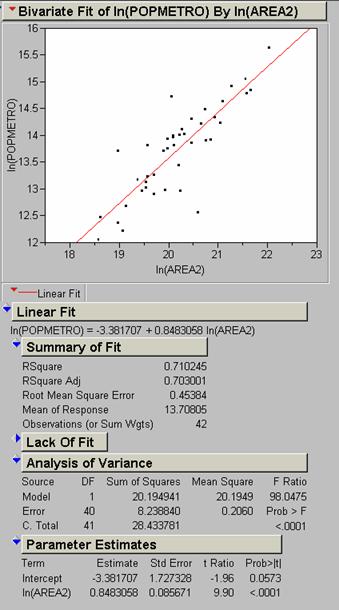
3)   Color code your points so that points representing cities in countries with GDP/capita less than $1000/yr are red, $1001-$5000/yr are blue, and over $5000/yr are green.  Run the same regression on Ln(Area2) and Ln(total population).  Describe the results.

 

 

I deleted rows that did not have PopMetro, and GDP/capita values before running the regression.  I was able to find a way to color the points and the corresponding regression lines.  Create a new column called GNPCODE and populate it with the formula below:

 

 

 

 

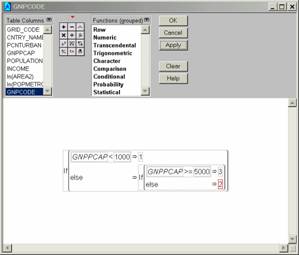
            In the regression set up proceed as usual but select Group results by GNPCODE. 

            The resultant regression yields interesting results:

 

 

 

The rich get richer and the poor get poorer?
 

 

 

 

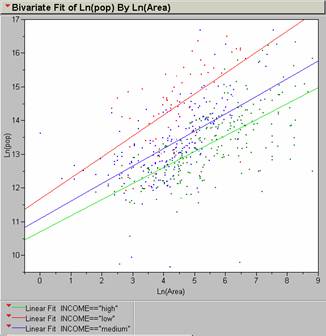
            The red curve is for GDP/capital less than $1000, the blue for GDP/capita from $1001-$5000, and the green is for over $5000. 

 

a.       The population of  “red” individuals falling into the lower group is greater than all the other groups.  “Green” individuals are the smallest of the three groups on a worldwide basis.

b.      The number of  “red” individuals increases faster with area than the other groups.  Regression slopes are steeper for this group.

c.       The number of “blue” individuals falls as area increases, possibly implying that some of the “blue” group becomes part of the “red” group as urban areas increase.

d.      Proportion of “green” individuals remains fairly constant as area increases. 

e.  The spread between the “reds” and the “greens” increases with greater area.

 

 

 

 

           

  The three regressions coefficients were:

 

 

 

GDP/capita $1001-$5000/yr
 
                      

 

The strength of the correlations varied for each group.  This might be an outcome of instability due to the small size of the dataset. 

 

After the bad instances were rejected from the table there were only 63 instances of “red”, 191 “blue”, and 244 “green.”  This is low for a dataset that should represent all significant world cities.

 

There should be many more “red” individuals than “green” individuals in the cities of the world.  This assumption is borne out even by the limited dataset available here; lowest levels show the most under-representation.  Possibly, this might be due to unreliable census results from poorer countries if the rest of the data is generally valid.
 

R2 = .315424   “red”

R2 = .385845  “blue”

R2 = .444432   “green”
 
   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

There are numerous other factors controlling the proportions of high GDP individuals than area.  Commercial centers might attract a greater numbers of this population relative to the total population than large cities with agricultural bases.

 

 

 

5)  Assume you only had the regression knowledge from the previous exercises and you had to estimate the populations of Mumbai, India, London, England, and Cali, Columbia from only their aerial extent as measured on the nighttime satellite image…

 

 

Global Model

 

Chandigarh, India (Mumbai didn’t make it into the table)

Area = 30 km2

            ln(BestPopEst) =11.521928 + 0.3949183 (lnCount2) = 12.8651

            Population inference = 386,591

 

            Cali, Columbia

Area = 172 km2   

            ln(BestPopEst) =11.521928 + 0.3949183 (lnCount2) = 13.5548                    

            Population inference = 770,469

 

 

            London, England

Area = 1,199 km2

ln(BestPopEst) =11.521928 + 0.3949183 (lnCount2) = 14.3216                    

            Population inference = 1,658,790

 

           

 

GDP/year Models

 

 

            Find out where they rank in GDP/year and then match the regression curves to come up with an estimate of population by inferential statistics.

 

           

            Chandigarh, India (Mumbai didn’t make it into the table)

Area = 30 km2

            GDP/year = < $1000

            ln(BestPopEst) = 11.67688 + 0.6232436(ln Count2) = 13.7967

            Population inference = 981,321

                       

 

            Cali, Columbia

Area = 172 km2   

                GDP/year = between $1001 - $5000

            ln(BestPopEst) = 11.093064 + 0.5191704(ln Count2) = 13.7655

            Population inference = 951,211

 

 

            London, England

Area = 1,199 km2

                GDP/year = > $5000   

ln(BestPopEst) = 10.702647 + 0.4756215(ln Count2) = 14.0744

            Population inference = 1,295,550

 

One would have to be very careful to get accurate polygon clusters for cities or weight them in some manner for country light variations.  Will use them and hope they are all off by the same factor.  Use the regression equation to estimate population and blame the errors on models that have poor R2 values.  These models don’t account for individual variations in specific cities.  The correlations vary from R2  values of .315424  for low-income nations  to .444432 for high income nations.  These are probably not the greatest predictors for population at the city level.

 

 

Global model –

 

To obtain 95% confidence intervals we incorporate the standard error of intercept and standard error of x in the regression estimate.

 

            Global Model—

 

            e(11.521928 + 1.96 (.151026) + (0.3949183 + 1.96(.029709))ln(Count2))  =  upper limit

            e(11.521928 - 1.96 (.151026) + (0.3949183 - 1.96(.029709))ln(Count2))  =  lower limit

 

            Chandigarh

 

            e(11.521928 + 1.96 (.151026) + (0.3949183 + 1.96(.029709))ln(30))  = 633,607 = upper limit

            e(11.521928 - 1.96 (.151026) + (0.3949183 - 1.96(.029709))ln(30))  =  235,876 = lower limit

At a population inference of 386,591 Chandigarh falls within the 95 % C.I.

 

            Cali     

 

            e(11.521928 + 1.96 (.151026) + (0.3949183 + 1.96(.029709))ln(172))  =  1,397,950 = upper limit

            e(11.521928 - 1.96 (.151026) + (0.3949183 - 1.96(.029709))ln(172))  =      424,650 = lower limit

At a population inference of 779,469 Cali falls within the 95% C.I.

 

 

            London

 

            e(11.521928 + 1.96 (.151026) + (0.3949183 + 1.96(.029709))ln(1199))  =  3,369,970 = upper limit

            e(11.521928 - 1.96 (.151026) + (0.3949183 - 1.96(.029709))ln(1199))  =      816,502 = lower limit

At a population inference of 1,658,790 London falls within the 95% C.I.

 

 

 

GDP/year models-

 

low GDP/year:  Chandigarh     

 

e(11.67688 + 1.96 (.517829) + (0.6232436 + 1.96(.114618))ln(30))  = 5,813,440 = upper limit

e(11.67688 - 1.96 (.517829) + (0.6232436 - 1.96(.114618))ln(30))  =     165,649 = lower limit

At a population inference of  981,321 Chandigarh falls within the 95% C.I.

 

 

           

medium GDP/year:  Cali          

 

e(11.093064 + 1.96 (.211773) + (0.5191704+ 1.96(.047321))ln(172))  = 2,322,120 = upper limit

            e(11.093064 - 1.96 (.211773) + (0.5191704 - 1.96(.047321))ln(172))  =     389,644  = lower limit

At a population inference of  951,211 Cali falls within the 95% C.I.

 

           

 

high GDP/year:  London

 

e(10.702647 + 1.96 (.191868) + (0.4756215 + 1.96(.034026))ln(1199))  =  3,027,640 = upper limit

            e(10.702647 - 1.96 (.191868) + (0.4756215 - 1.96(.034026))ln(1199))  =       554,373 = lower limit

At a population inference of  1,295,550 London falls within the 95% C.I.

 

 

 

 

6)  How could you use these regression models, a nighttime image of the world, and a % urban figure for every nation of the world to estimate the global population?

 

            Do the GDP appropriate regression estimate for each major city in a nation.

 

Sum each individual nation’s population estimates from the city level aggregations.  Estimate each nation’s population based on the percent urban:

 

                        total national population = (100 * urban population) / (% urban)

 

Sum these estimates for all the nations in the world.

 

 

 

 

 

 

ANALYSIS OF UNITED STATES DATA

 

 

Import in the prepared clusterareasumpop table to JMP.  This table was prepared by making a cluster id polygon table based on light values.  These polygons were then combined with the PopDen grid and summarized to produce a count of population density per cluster polygon.  Since each cell is 1 km2 we know the area directly.  The population numeration comes from the PopDen grid values.

 

7)  Produce a histogram of the population density data.  Some unusually high value outliers are causing the PopDen data to be poorly scaled. I deselected the highest values in ArcView to get a better display.  I’m assuming that these histograms show count levels for each value.                       

 

 

population density

 

 
 

 

 

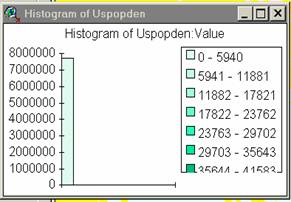
            The greatest majority of values fall in the range from 0-5940 for the United States.

 

 

 

8)  Produce a histogram of the Usatnight data.

 

 

 

Usatnight

value
 
   

 

 

 

 

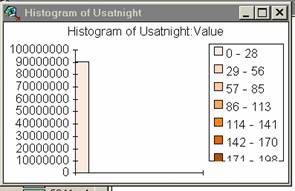
9)  These histograms show that the distribution of light pixels (1 km2 ) of specific values generally reflects the distribution of population densities.  Since lights vary with population the distribution of specific light values reflects the distribution of population densities.  In general, the histograms of light values and pop values correspond, suggesting that nighttime light values might be an acceptable proxy for population density.

 

 

 

10)  Produce a correlogram of the pop density data.

 

 

 

 

offsets in x for PopDen
 

 

 

 

 

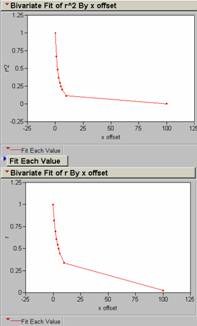
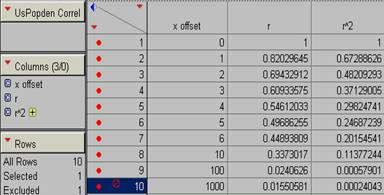
offsets in y for PopDen
 

 

 

 

 

 

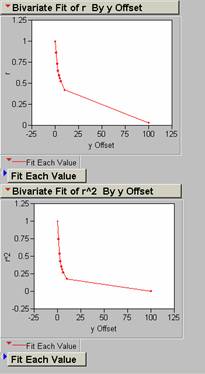
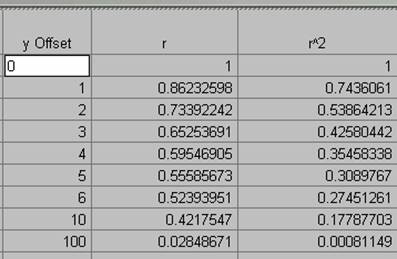
offsets in xy at a 450 angle for PopDen
 
                       

 

 

 

 

 

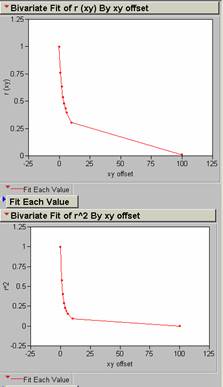
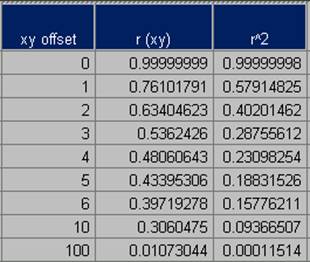
11)   Produce a correlogram of the Usatnight data.

Offsets in x, y, and xy (450) for Usatnight.
 
0

 

 

 

 

 

 

 

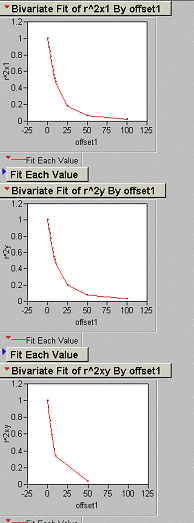
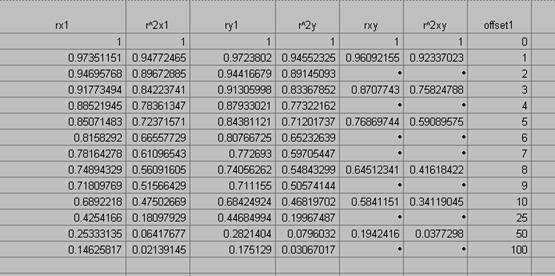
12)  An offset of one pixel (1 km2) in the x, y, or xy direction results in an average decrease in R2 of 33% for the population density grid.

 

 

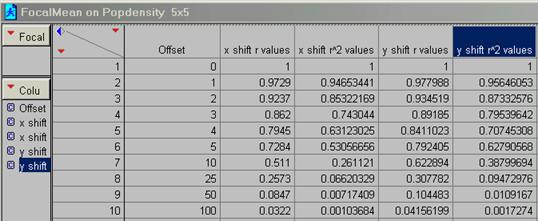
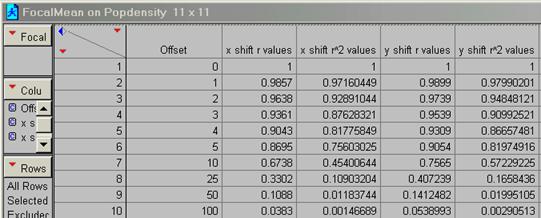
13)  Run a FOCALMEAN on the pop density data (use a 5 x 5 and an 11 x 11 filter).  Now generate two new correlograms for the ‘smoothed’ data.  How does FOCALMEAN work and how does it change the data?

 

 

              

 

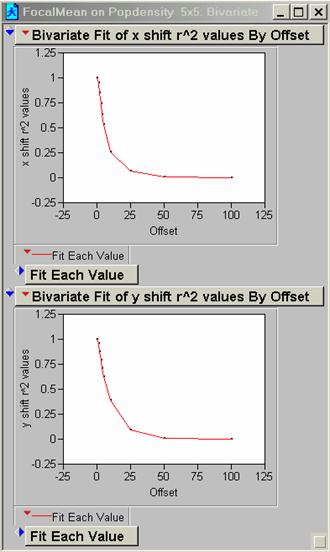
5 x 5 R2

 

 

 

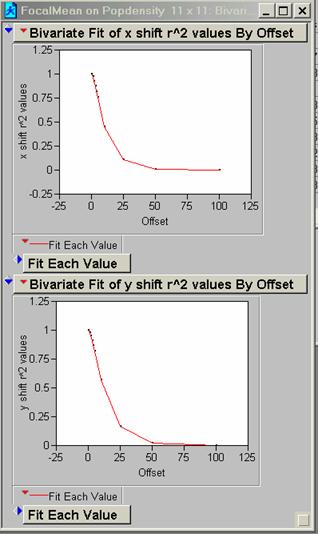
11 x 11 R2

 

 

FocalMean is a spatial filter.  The user specifies the number of pixels and shapes to average over and this average value replaces the original centered pixel value in the grid.  The net effect is to take out the high frequency variations in the data set.  After running FocalMean the correlogram should show an improvement in proportion to the size of the sample grid.  The 11 x 11 matrix is a more severe filter than the 5 x 5 matrix.  These relations are seen when we compare the 5 and 10 pixel offsets in the x direction for PopDen before and after smoothing:

 

R2    / pixel shift

PopDen no filter

FocalMean 5 x 5

FocalMean 11 x 11

5

.24687

.53057

.75603

10

.11377

.261121

.45401

 

I’m not sure that removing the high frequency portion of your data is a good idea, although the areal filters specified in pixel groups of 5 or 11 are not all that severe with regard to the total area and may serve to reduce noise or meaningless variations.

 

 

 

 

 

 

 

 

 

 

 

 

14)  Perform the same Ln(Area) vs. Ln(Population) regression on this data.  How is it different than the results for the U.S. from the world-level analysis?  Describe these results and the differences from the U.S. results in the world-level analysis.  Which regression parameters do  you think are more accurate?  Does this U.S. level study weaken or strengthen the argument that the areal extent of a city as measured by the DMSP OLS satellite is a good predictor of that city’s population?

 

 

U. S. data only, n = 6347
 

 

 

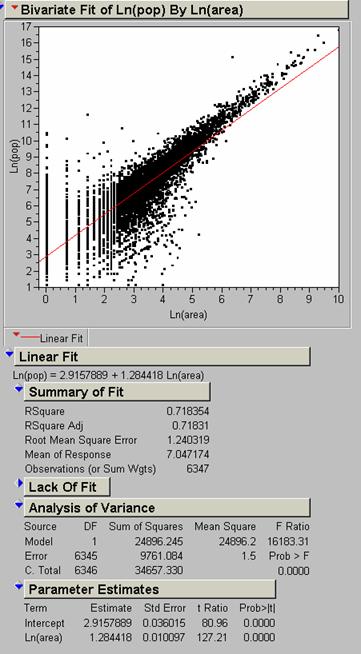
R2 values for the world are lower than for the U. S. except when we compare the “poor” or “red” segment of the world population with the U. S.  In this case the U. S. R2  value is significantly better than the world value, .718354 vs. .444432 

US subset of World Data.
 

 

 

I selected the United States instances from the world data and ran the regression again.  Only 42 instances were useable.  On the world “green” analysis there were 133 “rich” countries so one should be careful making comparisons on GDP/year information.  On the new US subset regression the R2  = .710245.  This is a significant correlation and is somewhat better than that obtained by using the “rich” set in the world data (R2 = .444432), but the significance is poor for the “rich” set because of the very low number of samples (n = 244).   The regression model for the U. S. subset is a little weird at the extreme since it indicates that areas below a certain limit have zero population.  A good general inferential population model would have to provide valid predictions across the entire scale and not just good values where the points are concentrated.

 

Our main problem is not in getting a high correlation, but in deciding if area is a good predictor of population density.  Since area is derived from the extent of lights we need to decide if lights themselves are a precise indicator of population density.  In the United States brightly lit areas generally coincide with population centers, but not always in a simple one-to-one variation.  You find brightly lit areas where the population density is low, e.g., along freeways and malls.  In suburban areas some communities make efforts to limit the amount of light pollution emitted.  There are numerous industrial centers that may be brightly lit but the population is transient and only there during the day.  Overall, I think that the new U. S. regression estimate is much better than that for the world because n = 6347 and you have less cultural complexities in the data set.  Remember that we were comparing several very different countries even when we limited are data selection to “rich” or “poor.”  Both Saudi Arabia and England fall into the high GDP aggregation but they may have very different cultural factors affecting the relation between lights and population. 

 

I think that the DMSP OLS imagery is excellent for predicting population because in the main, lights are a good proxy for population.  One would also have to be careful to adjust the data and interpret it correctly when trying to estimate population for individual nation aggregates. 

 

 

15)  Use the CORRELATION command in grid to get a simple correlation coefficient between the U. S. population density grid and the Usatnight record.  Record this R or R2.  Comment on its value and provide an explanation.

 

            The R2 value is .241931.  This is a fairly low value showing poor covariance.  Reasons probably might include such things as the PopDen data coming from a cruder sampling interval than represented by the nighttime lights coverage.  The satellite imagery records a rather continuous data stream, only degraded by the 1 km pixel dimension; the PopDen has been derived by census sampling and then aggregation.  Each aggregation unit probably covers much more than 1 km. The sampling procedure used in gathering the census data is much poorer quality than the information provided by the scans of lights.  Other reasons may be data that comes from two different dates.  This is also the general question, to what degree does light reflect population at the scale we are interested in?  This could be a root cause of poor correlations in localized areas.

 

 

16)  Model building:  Build a better model, describe/define it, justify it, and evaluate it.  Describe how it compares to the simple aforementioned model.

 

            The most obvious immediate way to get a better model is to go through the table and through out weird outliers or data that doesn’t make sense to produce a better input, although I think that the sheer quantity of good data in the U. S. table minimizes these kinds of problems.  I wonder if limiting the data collection to a particular day in the week would affect the data for smaller aggregations.  I think the data now includes a mixture of different time periods.  A smaller pixel resolution wouldn’t increase the accuracy of the data because the accuracy is limited largely by the population density aggregation level and data quality.  What happens when the pixels get much larger than the population density study aggregates?  Is the linear relation and the log data the best model method?  Perhaps there exists a non-linear fit that might do a more precise estimation and we should spend some time looking at more complex regression curves, although I’m glad we don’t.  Another alternative would be to build our linear regression model on a single representative city, adjust it to reflect real population density, and then apply it to the entire country.  We would have better confidence in what the numbers “mean” than the model computed over the entire light grid.   

 

            It would be neat to repeat the study every ten years or so for selected cities in the U. S. and see if one could match light changes with census population estimates.  A more precise model could be built and then applied to the general U. S. data. 

 

            Out present model depends on the degree to which nighttime lights vary with population density.  If we could find a better proxy than lighting we could produce a more precise model, especially over smaller city-size areas.  One might consider pollution emissions, car or gun registrations, welfare applications, number of first graders entering school, number of physicians, mall areas, or number of roadways converging on a city.  None of these would be easy to gather, compared to satellite reconnaissance, and the models would be much more complicated than even these regression equations and would not provide the possibility of gathering the data for the entire country.  If we tried to combine lights with some other more complex indicators we probably limit the generality of the models.

 

 

 

 

 

ANALYSIS OF LOS ANGELES DATA

 

 

            For this analysis I followed the procedure used to produce the Albuquerque city analysis, which follows later.  The general idea is to find a linear relation between a known population density coverage and a nighttime light set.  In this instance we had two population density coverages available, LAPOPDENSITY, and LAJOBDENSITY.  The first coverage represents residence based density and the second is employment based population density.  For our model we wished to approximate ambient population density so a new grid was produced, LAAMBIENT, which is a simple average of LAPOPDENSITY and LAJOBDENSITY. 

 

            In ArcInfo I used the SAMPLE function to produce an ASCII text file.  The text file contains the x and y coordinates and respective cell values of any two selected grids.  You can also apply a mask if necessary to limit the sampled area.  Masking is important to limit the size of the data set and to eliminate outliers that you do not want influencing the analysis.  This text tables allows one to run a regression between the LAAMBIENT and LANIGHTRADCAL coverages.  The LANIGHTRADCAL set consists of the low gain light acquisition coverage with a radiance adjustment.

 

17)  To apply the model I used the regression equation obtained from JMP:

 

            LADENEST = 168.21918 + 7.8361837 (LANIGHTRADCAL)

 

 

 

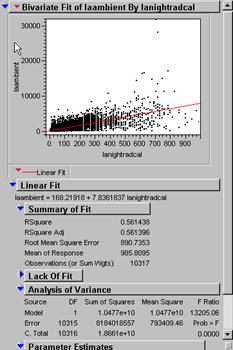
R2 = .561396  then R necessarily must be .748596.  I wonder is this would be close to the R-value you would get by the ArcInfo zero-lag spatial correlation of grids LAAMBIENT and LANIGHTRADCAL.  Grid pixel summing essentially predicts the proportion of total variation in one grid explained by the other.  The actual value using the function CORRELATION (lambient, lanightradcal, 0, 0) = .5932264054485 for a R2 –value of  .593226.  The pixel-to-pixel summing correlation is a different process than the line fitting used in the regression estimate.

 

Correlations of new model LADENEST to population density grids at 0 x, y shift:

 

Cover

Cover

R value

R2  value

LADENEST

LAPOPDENSITY

.5397405925319

.29132

LADENEST

LAJOBDENSITY

.4693194788425

.220261

LADENEST

LAAMBIENT

.5932264061103

.351918

 

 

 

18)  The best correlation occurred with the  LAAMBIENT average grid, but the R2 value of .3519 is nothing to write home about.  This LAAMBIENT average grid is a measure of the ambient population density and therefore the model is a better predictor of this aggregation than it is of the other two population densities.  It is still not a great predictor since a perfect model would have a R2 (or autocorrelogram unit value) = 1.0.

 

19)  I used ArcInfo to estimate the error by subtracting the individual population density grids from new model,  to produce error grids.

 

            LAERR = LADENEST - LAAMBIENT

 

            LAPOPDENERR = LADENEST - LAPOPDENSITY

 

            LAJOBDENERR = LADENEST - LAJOBDENSITY

 

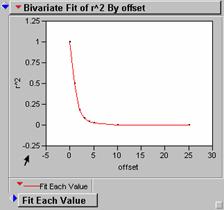
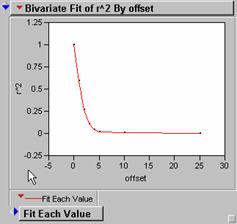
Below are the R2 correlograms for each of these new grids, shifted in x only, generally out to 25 pixels (25 km), which is probably a little excessive.

 

 

LAERR
 

 

 

 

 

 

 

LAPOPDENERR
 

 

 

LAJOBDENERR
 

 

 

 

 

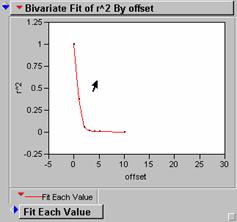
These correlograms have very steep drop off rates as the grids are translated along the x axes.  This indicates that there are lots of high frequency spatial variations in the data and could be a sign of poor agreement between model and individual grid.  R2 values for these seem lower than what we would like to see if the model was effective in inferring population density from light intensity values.

 

 

Visualization of autocorrelation error:

large magnitude of error with

high frequency variation over distance
 
 

 


                                                                                                           

error grid   ____________________________  

distance

 
 
 


           

 

            Result of this autocorrelation would be lower normalized r-values past the initial one and faster drop off on correlogram.

low magnitude of error

low spatial variation
 
 

 


error grid  _____________________________

distance

 
 
 


                                                           

 

            Result of this autocorrelation would be high normalized r-values past the initial one and slower drop off on correlogram.  This is what we want to see in our error grids.

 

            It seems to me that we are seeing the first instance and not the situation shown in the second diagram.

 

 

Follow on the next page are displays of the error grids and their histograms.

 

 

 The red areas are indicative of areas where the model overestimated the population densities; the blue areas show underestimates.  The worst error is concentrated in the densest downtown area.  The model apparently does not work well in downtown Los Angeles.  Overall there are substantial amounts of values falling into the ranges of +/- 3 standard deviations.  The least amount of visual error in associated with the LAJOBDENSITY coverage and the worst visual representation occurs with the LAPOPDENSITY cover.  The larger amount of error with LAPOPDENSITY implies that this grid does not agree well with the LAAMBIENT average.  This means that there is less difference between the LAAMBIENT and LAJOBDENSITY grids than exists with the LAPOPDENSITY.  Does this mean that job based densities are “over weighted” relative to residences, i.e., they have constant high density levels that do not vary because of movement between residential areas and industrial areas. 

 

Which residual error grid has the smallest mean absolute deviation?

           

            I obtained the actual standard deviation by running the SAMPLE function in ArcInfo on the three overages, and then bringing the resulting text table into JMP.  There is probably an easier way to do this in ArcView.  It is then possible to get the standard deviation and histograms of the error residuals.

 

 

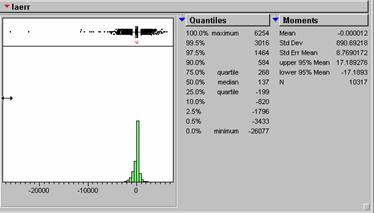
Grid

Standard Deviation

LAERR (model – ambient average)

890.69218

LAPOPDENERR (model – lapopdensity)

1247.1901

LAJOBDENERR (model – lajobdensity)

1179.9465

 

The LAERR layer, produced by subtracting the LAAMBIENT cover from the LADENEST population density model has the lowest absolute standard deviation.  This makes sense since the LAAMBIENT coverage was used to produce the model.

 

 

 

ANALYSIS OF ALBUQUERQUE DATA              

 

 

            We decided to apply the LA style analysis to the city of Albuquerque NM.  This city is interesting because it is one of the faster growing cities in the southwest and has been the subject of much recent research about urban expansion in New Mexico by the USGS.  Our available coverages were all for the entire U. S. and included the Usatnight lights and the Uspopden grids.  We used the Usalazea to figure out where we were.  Once the desired city’s light pattern was located on the Usatnight grid, we needed to outline and clip the larger light grid to include only the city.  Our procedure was as follows:

 

Starting with the Usnightbinary image of the Usatnight we clipped the image to the correct areal city coverage.   

 

Run REGIONGROUP to build polygon coverages with unique number ids.

 

Produce a mask by running:  maskgrid = SETNULL(region_group_output ne 1, 0), you will have to figure out which polygon value belongs to your city.  Setnull makes every value not equal to your city value == 0.  This gets rid of every light concentration accept the one you specifically need.

 

Apply the mask to the population density:  Albuquerquepd = Albuquerquemask x Uspopden.

 

Apply the mask to Usatnight:  Albuquerquenight = Albuquerquemask x Usatnight

 

When all these manipulations were accomplished we had three grids:  Albuquerque mask, Albuquerque population density, and Albuquerque nightlights and were ready to carry out the regression modeling.

 

            Next we ran the SAMPLE function to produce a text table of xy values with their associated grid values for the clipped light and population density coverages.  This table went into jump and a regression equation was derived.  This equation uses the light values to estimate the population density values.  Running the regression equation on the Albuquerque nightlights grid produced the Albuquerque population density model grid.  Subtracting the derived model grid from the actual population density grid made display of error.  The error grids were classified using standard deviation and then plotted on the attached display.  (Note – Alex and I did the Albuquerque ArcInfo analysis together.  After the analysis he gave me a copy of the display he produced and I shamelessly incorporated it into my lab.  Hope this is OK.)

 

            Albuquerque error displays show the same problem as in the LA dataset.  The worst under and overestimates seem to occur where population is most dense.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Making Sense of Spatial Grids and Time Series Analysis (Trying to see the trees in the forest!) --

 

Many of the terms used in the analysis of spatial data and time series are similar.  In time series analysis we are interested in discriminating against those portions of the composite waveform that are don’t contain useful data and in enhancing those portions of the signal spectrum that do contain meaningful information.  The discrimination is done by low- or high-pass filtering operations.  These operations can be done either in the time domain or the frequency domain.  These two domains are transformations of one another, done by means of Fourier analysis.  Fourier analysis lets us decompose a signal into its single frequency components.  No attempt seems to be made in improving the quality of spatial data after it is acquired, but in time series analysis no one would ever accept the raw data and use it to make inferences.  Is data from the light sensing satellites so clean that it doesn’t need additional work?  What could be some of the sources of noise in the light data set?  Some of these are reduced because I think that the satellite accumulates lights over time.  This acts as a low pass filter and discriminates against random light flashes.  This process also reduces the amount of information in the intensity values as things get averaged. 

 

 We accept the idea that any naturally occurring time series (e.g., earthquake p waves) is composed of varying amounts of both signal and noise and make a determined effort to build up signal at the expense of noise.  The most straightforward technique is to simply filter off noisy components if they are aggregated in a single or narrow frequency band.  A high-pass filter keeps the high end of the components and rejects, with varying success, those noisy low frequency components.  Similarly, a low-pass filter would attempt to reject high frequency noise.  Notch filters try to reject or pass a very narrow frequency band. 

 

Another technique used to remove repetitive information from a signal and improve the signal to noise ratio is spike and predictive deconvolution, special types of correlation.

 

On the other side of frequency rejection, it is a common exercise to increase the relative proportions of useful data by employing spectral whitening procedures.  These can be done in either the time or frequency domains.  In spectral whitening, we try to equalize all the frequency components in our zone of interest.  In a sense we are trying to get rid of the normal frequency distribution.  The high frequency components allow us to make the most precise measurements.  They are the most valuable and of course, the hardest to obtain, since high frequency waves are the most easily scattered and are attenuated by the time they get to the sensor.  They can be restored however, with some success. 

 

What does this have to do with spatial data or grids?  Time series are a two dimensional reference frame in which the components are amplitude and time.  In the case of the frequency domain the components are amplitude and frequency.  Grids are multidimensional reference frames in which the components are length and width with a third dimension of magnitude.  In a sense grids are the same as time series without the directional nature imposed by time.  Do we have to do our analyses on histograms?  That would be a dead end because we cannot restore the pixels to their correct spatial locations.  We could run standard time series operations (that we can visualize) on histograms and then re-transform the resulting values to the grid reference frame.  A histogram of a grid is a transform from space to something like a time series (amplitude versus dimensionless distance (?), it doesn’t matter).

 

In time series analysis we are concerned with the sampling of the signal.  The sampling interval of discrete digital values determine the frequency of the data we can collect.  This required sampling interval is determined by the Nyquist formula that states that sampling rate must be twice the highest frequency sampled.

 

Do these concerns have anything to do with spatial datasets?  I think they are inherently noisier than we believe.  In spatial datasets the sampling unit is the pixel, not the second.  Pixel size seems to work just like sampling intervals in time.  The larger the pixel size, the less high frequency spatial information we recover.  In nighttime lights analyses we are concerned with the size of the blobs, but the big blobs are aggregations of small blobs.  The small blobs contain information.  Would it be valuable to be able to reconstruct the values of the small blobs and separate their values from the larger  aggregations or is the amount of “smear” a function of population density.   The pixel size limits the amount of information we can get from the small light variations.  There are still high-frequency variations within the big blobs but they may be buried by the more intense light inputs from the bigger light sources.  Can a kind of spectral whitening be applied to the big aggregations to restore the high-frequency information?  Better resolution and discrimination might mean improved regression models.

 

 What does the (supposed) binary step gain used in the satellite end of the data acquisition process do to the input data?  Large values are scaled down and weak values are pumped up.  There are threshold limits at both ends of the data.  I don’t have a good idea of the raw dynamic range of the nighttime lights signal.  At least very high values are reduced to a huge degree.  Surely we lose information about light intensity by the gain values filter put on the data by the satellite.  What is the range of the output signal, 1 - 256?  Is this a valid representation of the actual light intensities?  Our models have to take this limitation into account by default.  Better, more representative data, might be an easy way to improve the models.  To me, it seems that this concern for gain problems is more important than pixel resolution, and more cost effective in terms of processing time.

 

 

Questions About Correlation --

 

      Correlation, especially autocorrelation, is an important technique of traditional signal analyses.  Cross-correlation is commonly done to recognize similarities between two or more input signals.  The result of a cross-correlation between two identical signals (autocorrelation) is a Weiner-Levinson autocorrelation or recognition spike, the width of which is determined by the frequency components of the input signals, assuming that the wavelets are zero-phase (non-skewed or zero skewed).  The central peak of an autocorrelogram wavelet is unity.  The width of the central output wavelet is relatively unimportant, it being a function of the average of the frequencies in the individual series.   What is important is the value or amplitude of the spike. This amplitude corresponds to our R-value. Incidentally, in time series, the convention is to display both sides of the autocorrelation function, not just half of it like we do in our correlograms.  We always start at zero-lag and work in just one direction, but there is no reason not to go both ways.  (Will the ArcInfo CORRELATION function accept negative x or y values?)  We would get a diagram that we are more used to working with.  The width (frequency) of the correlogram is wider for data dominated by low frequencies and narrower for high-frequency data.  Additional lobes on either side of the central spike are due to repetitive frequencies or “ringing” in the data set. One of the goals of traditional time series analysis is to remove those outer lobes though filtering and signal to noise enhancements such as whitening and deconvolution.  These side effects might be seen if we carried out larger translation shifts on our ArcInfo correlations.

 

 

Wave Number and Spatial Datasets --

 

            Another way of describing time series is by means of wave number or k.  Wave number is the number of waves of a particular length per unit distance.  k = number of waves per distance while frequency =  number of waves per time.  While wave number is not of much use in time series work, it might be a way to link up the ideas of time series analysis to spatial displays.  We have gotten around the constraint imposed by the time axis part of the display by replacing it with the spatial unit of distance.  Would this scheme help us visualize and apply time series techniques to spatial grids?